At beregne areal er en grundlæggende koncept inden for forskellige fagområder som arkitektur, ingeniørvirksomhed og matematik. Det giver os mulighed for at bestemme størrelsen af todimensionelle former og spiller en afgørende rolle i at løse virkelige problemer. I denne artikel vil vi udforske forskellige metoder til at finde arealet og forstå deres anvendelser.
Forståelse af Areal
Areal henviser til mængden af plads, der besættes af en todimensionel form. Det måles i kvadratiske enheder som kvadratmeter eller kvadratfod. At have en solid forståelse af konceptet om areal er afgørende for præcise målinger og beregninger inden for mange discipliner.
At finde Arealet af Basale Former
For at begynde vores rejse ind i arealberegning, lad os starte med de basale former:
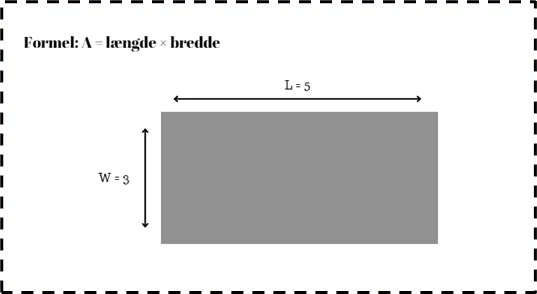
Areal af en Rektangel
Et rektangels areal kan bestemmes ved at gange længden og bredden. Formlen til at beregne et rektangels areal er A = længde × bredde. For eksempel, hvis et rektangel har en længde på 5 meter og en bredde på 3 meter, vil arealet være 5 × 3 = 15 kvadratmeter.
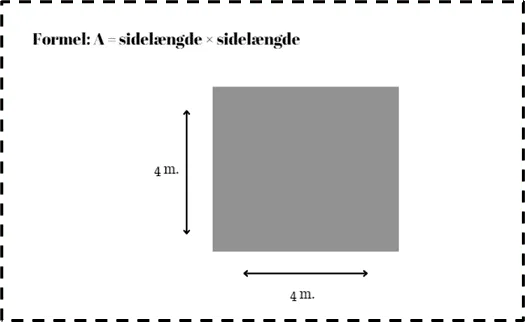
Areal af en Firkant
En firkant er en særlig type rektangel, hvor alle sider har samme længde. For at finde arealet af en firkant ganger vi længden af en side med sig selv. Formlen til at beregne arealet af en firkant er A = sidelængde × sidelængde. For eksempel, hvis en firkant har en sidelængde på 4 meter, vil arealet være 4 × 4 = 16 kvadratmeter.
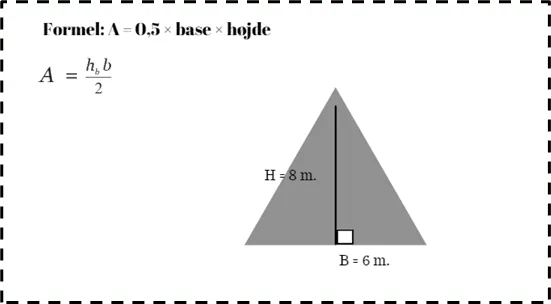
Areal af en Trekant
Areal af en trekant kan bestemmes ved at gange længden af grundlinjen med højden og derefter dividere resultatet med 2. Formlen til at beregne arealet af en trekant er A = 0,5 × grundlinje × højde. For eksempel, hvis en trekant har en grundlinje på 6 meter og en højde på 8 meter, vil arealet være (0,5) × 6 × 8 = 24 kvadratmeter.
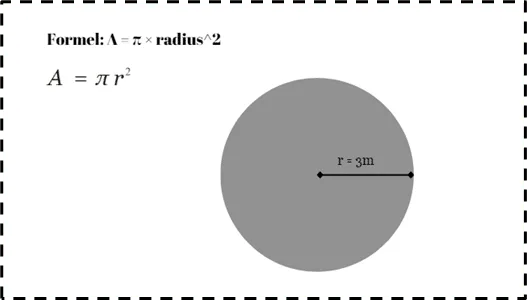
Areal af en Cirkel
Areal af en cirkel findes ved at gange kvadratet af dens radius med den matematiske konstant π (pi). Formlen til at beregne arealet af en cirkel er A = π × radius^2. For eksempel, hvis en cirkel har en radius på 3 meter, vil arealet være 3,14 × 3^2 = 28,26 kvadratmeter (cirka).
At Finde Arealet af Sammensatte Former
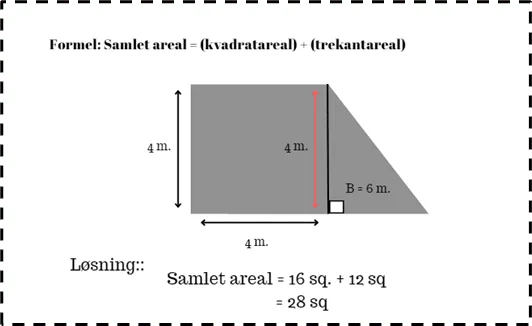
Sammensatte former dannes ved at kombinere flere basale former. For at finde arealet af sammensatte former opdeles de i enklere former, beregnes individuelt og summeres derefter for at finde det samlede areal. Lad os betragte et eksempel:
Forestil dig en figur bestående af en rektangel og en trekant. Vi kan finde arealet ved at beregne arealet af rektanglet og arealet af trekanten separat og derefter lægge de to arealer sammen.
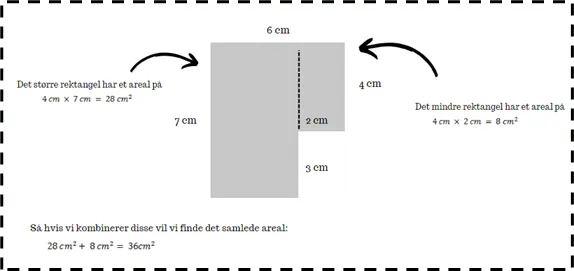
At finde arealer af uregelmæssige former
Uregelmæssige former har ikke en specifik formel til beregning af areal. Dog kan vi tilnærme deres areal ved at opdele dem i mindre, mere enkle former, hvoraf arealerne kan beregnes let. Ved at summere arealerne af disse mindre former kan vi opnå en tæt tilnærmelse af den uregelmæssige forms areal.
Avancerede teknikker til beregning af areal
I avancerede scenarier, hvor formen er kompleks eller ikke passer ind i grundlæggende kategorier, kan vi bruge calculus til at finde arealet. Calculus indebærer at integrere formens ligning for at opnå arealet. Selvom denne teknik ligger uden for denne artikels omfang, giver den en kraftfuld metode til at beregne areal i mere udfordrende situationer.
Nu, øv dine matematiske færdigheder
At beregne areal er en essentiel færdighed, der finder anvendelse inden for forskellige studieområder og i dagligdagen. Ved at forstå formlerne og teknikkerne til at finde arealer af grundlæggende former, sammensatte former og uregelmæssige former kan vi foretage præcise målinger, løse problemer og træffe informerede beslutninger. Øv dig og anvend den viden, du har opnået gennem denne artikel, og du vil være godt rustet til ubesværet at finde arealer i forskellige scenarier.