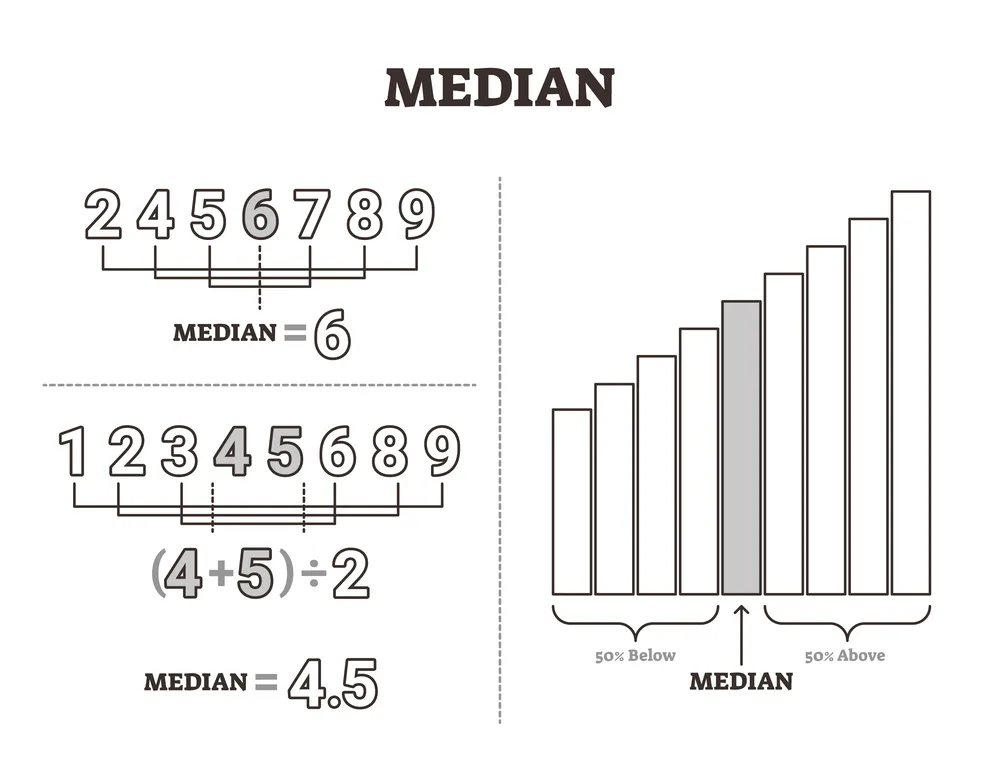
Tallet i midten
Men i virkeligheden er en median mere end det. For der er nemlig forskel på, hvad begrebet helt præcist dækker over, alt efter om der er tale om statistik eller trigonometri. Når det gælder medianer, er det vigtigt at skelne mellem såkaldte grupperede og ugrupperede datasæt. Eller såkaldte ordnede og uordnede. Dette har nemlig en afgørende betydning. I praksis betyder det, at når man skal finde medianen, er det vigtigt først at sortere den givne talrække, så det er muligt at finde tallet i midten af den pågældende række. Det betyder at er der syv tal i en række, for eksempel 1, 2, 3, 4, 5, 6, 7, så er medianen 5. Altså tallet i midten. Er der derimod tale om en talrække som 2, 3, 3, 5, 7 og 10 er medianen lig med 4.
Medianen sat på formler
Der findes en række formler til udregning af medianer, som kan være yderst anvendelige. Ikke mindst hvis der er tale om en længere talrække, hvor der kan være svært at gennemskue nøjagtig hvad midten er uden at skulle tælle efter. Her er det imidlertid vigtigt at være opmærksom på, at en median ikke er lig med et gennemsnitstal. Derimod anses medianen ofte som værende mere gældende og et bedre udgangspunkt end et simpelt gennemsnit.